Quantum Key Distribution(QKD) is a secure communication method that utilizes quantum mechanical properties to implement cryptographic protocols. It enables two communicating parties to produce and share a random, secure key for encrypting and decrypting messages. It is often misnamed quantum cryptography, as it represents the most prominent example within the field of quantum cryptographic tasks.

One of the most crucial and distinctive properties of quantum key distribution is that if any third party attempts to eavesdrop on the key, both communicating parties will detect it. This property stems from a fundamental principle of quantum mechanics: any measurement of a quantum system inevitably disturbs it. To intercept the key, a third party must perform measurements in some manner, and these measurements introduce detectable anomalies. By transmitting information through quantum superposition or quantum entanglement states, the communication system can ascertain the presence of eavesdropping. When eavesdropping falls below a certain threshold, a secure key can be successfully generated.

Below is a circuit implementing quantum communication using qiskit

from qiskit import QuantumCircuit,  transpile
from qiskit_aer import Aer
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from numpy.random import randint
import numpy as np

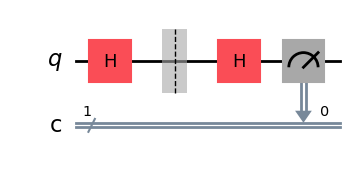
qc = QuantumCircuit(1,1)
qc.h(0)
qc.barrier()
qc.h(0)
qc.measure(0,0)

display(qc.draw('mpl'))
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
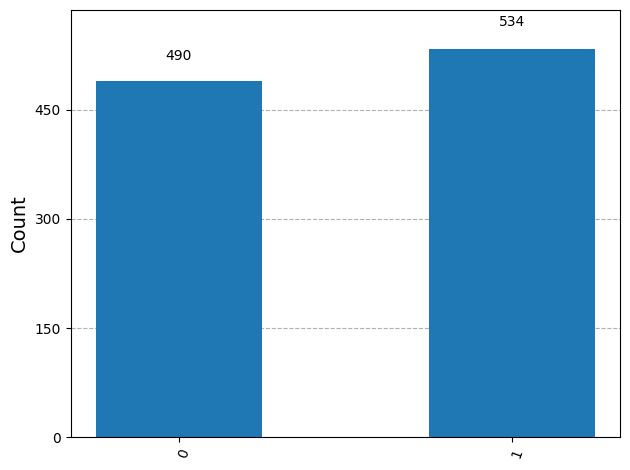
plot_histogram(job.result().get_counts())

We can clearly find that Bob’s measurement of the quantum bit sent by Alice has one and only one outcome.

Let’s see what happens when there’s third-party eavesdropping?

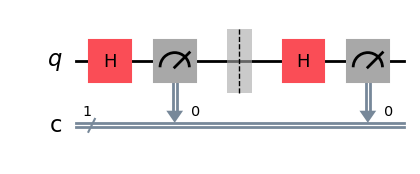
qc = QuantumCircuit(1,1)
qc.h(0)
qc.measure(0, 0)
qc.barrier()
qc.h(0)
qc.measure(0,0)

display(qc.draw('mpl'))
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
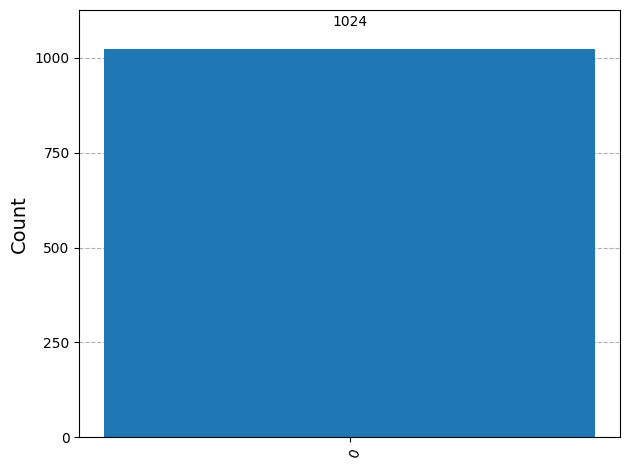
plot_histogram(job.result().get_counts())

The quantum state that Bob listens to changes, and the messages he receives become 0 and 1 with a 50% probability each.